Code Optimization with Single Instruction, Multiple Data

Strong Arm Performance

Coding for the ARM NEON vector hardware can significantly improve performance and help you get the most out of low-power systems such as the Raspberry Pi.

You have just coded that new algorithm, the one that handles all the complexities of your data to return exactly the answers you need. As you launch the program and wait, you realize that you have a problem: You are still waiting. The code is slow, far too slow to be usable. You need faster processing, preferably without upgrading your hardware.

Before you reach for the other cores on your processor, it makes sense to see if you can optimize the code for a single core first. Any single-core optimizations will reduce the number of cores ultimately needed. Taking advantage of any available single instruction, multiple data (SIMD) hardware is an effective means of accelerating mathematically intensive problems. SIMD (vector) hardware uses parallel arithmetic units executing the same operation on multiple elements of data within the same clock cycle.

ARM’s implementation of SIMD, called NEON, is relatively intuitive and effective. The NEON instructions operate on 128 bits (16 bytes) of data per clock, either as sixteen 8-bit characters, eight 16-bit short integers, or even four 32-bit floating-point numbers. Modern compilers, such as GCC, have the ability to vectorize code automatically during optimization, but you often have room for improvement if you are willing to use the NEON instructions directly.

Intrinsic functions that map to the underlying NEON instructions are available in the GCC compiler, enabling assembly-style programming of NEON operations with the overall conveniences of the C (or C++) language. The intrinsic functions and NEON data types are available with the

#include <arm_neon.h>

directive in the C code. It can take practice and a fair bit of imagination to master the data manipulation needed for effective SIMD coding, but the performance gains justify the effort. 

The Algorithm

The best way to learn SIMD vector coding is on real problems with simple but non-trivial algorithms that demonstrate a variety of SIMD techniques. The example algorithm

for n in [0,N)
  y[n] = Ax^3[n] + Bx^2[n] + Cx[n] + D
return(max(y),argmax(y))

evaluates a third-order polynomial, but rather than return the resulting values, the maximum of the result and its index (argmax) are returned instead. The values of the input array x are randomly generated, so you cannot exploit any specific ordering.

Scalar Code

The first step to writing the vector code is to create a scalar (i.e., standard) C code implementation of the algorithm, which provides a reference implementation against which to validate the eventual vector code. The x and y values are represented as 32-bit floating point, which is realistic and enables good NEON improvement.

The findMax() function in Listing 1 takes in the number of elements (N) and a pointer to the input array (xval). The return value is a structure that holds the maximum value and its index. A single loop evaluates the polynomial formula for each entry of the xval array, storing it to a temporary value. To implement the max and argmax functions in this same loop, each output value is checked to see whether it is larger than the current maximum stored in the return structure. If so, the value and its index are stored in the return structure.

Listing 1: findMax() Scalar Code

typedef struct{
               int   ind;
               float val;
              } maxret_t;

maxret_t findMax(int N, float *xval)
{
  int n;
  float x, x2, x3;
  float val;
  maxret_t mret = {‑1, ‑1.0e38};

  const float A = 0.052;
  const float B = 0.24;
  const float C = 3.3;
  const float D = 10.1;

  for(n=0;n mret.val)
        {
          mret.val = val;
          mret.ind = n;
        } /* end if */
    } /* end for n */

  return(mret);

} /* end findMax */

The initial maximum is set to a significantly large negative value so that it is overwritten in the loop. Should the loop still fail to find a new maximum, the caller can check to see whether the returned index is set to -1, indicating this error.

Vector Code

The NEON version of the code, findMaxVec() in Listing 2, takes the same arguments as the scalar version. Inside the routine, the xval array pointer is recast to a float32x4_t pointer named vxa. This change does nothing to the underlying data; both xval and vxa point to the same address, but the float32x4_t type tells the compiler to treat the memory as an array of vectors when using vxa, with each vector consisting of four 32-bit floating-point values. The Nv variable is the number of complete vectors in the N length array. If N is not a multiple of four, Nv will not encompass the final few data points.

Listing 2: findMaxVec() Vector Code

maxret_t findMaxVec(int N, float *xval)
{
  int n;
  int Nv = N/4;

  float32x4_t vx, vx2, vx3;
  float32x4_t vtmp;
  float32x4_t *vxa = (float32x4_t *) xval;
  float       vfload[4] __attribute__((aligned(16)));
  int32_t     viload[4] __attribute__((aligned(16)));

  uint32x4_t  vmask;
  float32x4_t vmax;
  int32x4_t   vmxind;
  int32x4_t   vind = {0, 1, 2, 3};
  int32x4_t   vinc = {4, 4, 4, 4};

  maxret_t mret = {‑1, ‑1.0e‑38};

  const float32x4_t vA = {0.052, 0.052, 0.052, 0.052};
  const float32x4_t vB = {0.24, 0.24, 0.24, 0.24};
  const float32x4_t vC = {3.3, 3.3, 3.3, 3.3};
  const float32x4_t vD = {10.1, 10.1, 10.1, 10.1};

  vmax = vdupq_n_f32(mret.val);
  vmxind = vdupq_n_s32(mret.ind);
  for(n=0;n mret.val) ||
          ((vfload[n] == mret.val) &&
           (viload[n] < mret.ind)) )
        {
          mret.val = vfload[n];
          mret.ind = viload[n];
        } /* end if */
    } /* end for n */

  return(mret);

} /* end findMaxVec */

The first loop in the function iterates over the number of vectors (Nv), evaluating the polynomial with vector multiply (vmulq_f32) and vector multiply-accumulate (vmlaq_f32) instructions (Listing 3). The “f32” in the name indicates operation on 32-bit floating-point data. The “q” in the name indicates operation on the full 128 bits of the NEON vector. NEON instructions can operate on half vectors (non-q versions) but are not needed in this case. Here, all four of the 32-bit floats can be used for better acceleration.

Listing 3: Polynomial Evaluation

/* val = A*x3 + B*x2 + C*x + D; */
vx = vxa[n];
vx2 = vmulq_f32(vx,vx);        /* x2=x*x */
vx3 = vmulq_f32(vx2,vx);       /* x3=x2*x */
vtmp = vmlaq_f32(vD,vC,vx);    /* tmp = C*x+D */
vtmp = vmlaq_f32(vtmp,vB,vx2); /* tmp += B*x2 */
vtmp = vmlaq_f32(vtmp,vA,vx3); /* tmp += A*x3 */

The NEON unit has two multiply-accumulate instructions, the second one being the fused multiply-add (vfmaq_f32). The vfmaq_f32 version rounds the floating-point result after the accumulate, whereas the vmlaq_f32 instruction used here rounds after the multiply and again after the accumulate. As a result, the vector and scalar versions of the code might have small rounding differences when using either of these instructions.

Conditionals

To implement the max/argmax functionality, the polynomial values in vtmp must be compared with the running maximums in vmax. The vtmp and vmax vectors each contain four values. A conditional could have a different result for each element in the vector, which is not conducive to branching the code. The SIMD convention is not to branch, but to evaluate both branches of a conditional and combine the results with a conditional mask. The mask is set to all ones if the condition is true, and all zeros if false. The true result is bitwise ANDed with the mask, and the false result is bitwise ANDed with the mask’s complement. The two masked results are then added together for the desired output. This process is often called a select operation, and NEON provides the vector bit select instruction (vbsl) to implement it. The bit select pseudocode is

result = if(a==true)&result1 + if(a==false)&result2

Listing 2 shows the conditional logic in findMaxVec(). A vector greater-than instruction (vcgtq_f32) generates the bit masks for vtmp > vmax. This bit mask vector (uint32x4_t vmask) is used to drive two separate bit select instructions: one to update vmax and one to update the maximum index vmxind. The mask itself is of type uint32x4_t and operates with the bit select function for floating-point (vbslq_f32) and signed integer (vbslq_s32). The bit select argument order is mask, true answer, false answer.

Vector Initialization

To find the indices of the maximum, the vector loop must keep track of the scalar indices for the vector elements being operated on. This is accomplished by creating a signed integer vector (int32x4_t vind) initially set to the sequence 0,1,2,3. Each time through the vector loop, vind is incremented by a vector set to all fours (4,4,4,4) because each vector element, or lane, is striding through the array by four elements during the loop.

The vind and vinc vectors are initialized during the declaration statement with bracket notation:

int32x4_t vind = {0, 1, 2, 3};
int32x4_t vinc = {4, 4, 4, 4};
...
/* Bottom of the for loop */
/* Increment index values */
vind = vaddq_s32(vind,vinc);

This bracket notation for setting vectors is only available in the declaration statement, similar to the C language limitations for initializing arrays and structures.

When the vmax and vmxind vectors are initialized to the values of the mret structure,

vmax = vdupq_n_f32(mret.val);
vmxind = vdupq_n_s32(mret.ind);

all the lanes are set to the same value. The vector duplicate instructions (vdupq_n_f32 and vdupq_n_s32) generate vectors with all of the lanes set to the input scalar value. This initialization is placed before the for loop. 

Cleanup

If the input array length is not a multiple of four, the vector loop leaves up to three entries unprocessed. The vector loop itself results in four maximum and index values. The global maximum must be found among these partial results to match the original scalar function.

To handle any leftover data, you can run the scalar function findMax() where the vector loop left off, namely at an offset of 4*Nv:

/* Convert Nv count to scalars */
Nv *= 4;
if(Nv != N)
{
mret = findMax(N-Nv,xval+Nv);
mret.ind += Nv;
} /* end else */

The overhead of a function call is not ideal for a few samples, but it is worth the code simplification and is only called once. The scalar function is called with the proper offsets into xval (4*Nv) and size (N-4*Nv). The index value returned is relative to the offset data fed into it, so 4*Nv is added to the returned index. Notice how Nv is multiplied by four first to convert it from vector to scalar counts.

The individual elements of the vectors vmax and vmxind must be compared with the maximum in the return structure mret. Listing 4 shows the relevant instructions from the findMaxVec() function. The vector data is stored into regular C arrays to process them in scalar code. Two arrays, vfload and viload, are declared as four-element C arrays. The alignment of the arrays to 16-byte boundaries is not absolutely necessary for NEON. The vector store instructions (vst1q_f32 and vst1q_s32) move data from the vector variables to the scalar arrays. Note that the vector load instruction (vld1q_f32) was not explicitly used in the first loop because the data was accessed by a vector pointer to the allocated memory. The store into the vfload array could be accomplished with pointer casting, but would not be as legible.

Listing 4: Vector Cleanup

float       vfload[4] __attribute__((aligned(16)));
int32_t     viload[4] __attribute__((aligned(16)));
...
vst1q_f32((float32_t *) vfload,vmax);
vst1q_s32(viload,vmxind);
...
for(n=0;n<4;n++)
  {
  if( (vfload[n] > mret.val) ||
    ((vfload[n] == mret.val) &&
     (viload[n] < mret.ind)) )
     {
        mret.val = vfload[n];
        mret.ind = viload[n];
     } /* end if */
  } /* end for n */

The following lines are equivalent:

*((float32x4_t *) vfload) = vmax;
vst1q_f32((float32_t *) vfload,vmax);

The final four maximums are run in a small loop at the end of the routine. During testing, one complication came to light: The randomly generated xval arrays are not diverse enough to avoid duplicate values, so multiple copies of the maximum can be found from a single input array. The scalar findMax() routine returns the index of the first instance of the maximum in these cases.

In the vector code, the first maximum is not guaranteed to occur in the first vector element because of the strided nature of the computation (each lane of the vector sees every fourth array value). The final four comparisons must check to see whether the values are equal and, if so, select the minimum of the indices (Listing 4). With this in place, the vector code matches the scalar function results, except for some small rounding differences in the polynomial.

The Test Routine

The main routine can be found in full at the end of the article (Listing 9). This program is set up to run and profile both the scalar findMax() and the NEON findMaxVec() functions. The caller can specify the number of elements to test on the command line, but if they do not, the code will use 1024*1024+1 elements in each call to the functions (line 46), which equates to 4MB of memory in the input array xval. This size should be larger than the L2 and L3 caches of the test machines so they are forced to cycle data from DRAM on each iteration, rather than using only cache memory. The plus one in the count ensures the NEON code is executing the cleanup call to the scalar code.

Both functions use a 32-bit integer to track the array index, so the main function ensures the array is never large enough to roll over those indices (with plenty of margin). The xval array is allocated with malloc() and then filled with randomly generated floating-point data (lines 109-113). These random numbers are scaled from 0 to 10, with four fractional digits.

The inline function getTimeInSec() in Listing 5 is used to measure runtimes. The function encapsulates the gettimeofday() call to return time in seconds. Note that gettimeofday measures real time, or wall clock time, as opposed to the clock() function found in the C library, which counts CPU cycles. If the operating system suspends the application, the time suspended is not counted by the clock() function and can result in erroneously good profile times.

Listing 5: Time Conversion Function

static inline double getTimeInSec(void)
{
  double dtime = ‑1.0;
  struct timeval tv;

  if(gettimeofday(&tv,NULL) == 0)
    {
      dtime = 
((double) tv.tv_sec) + ((double) tv.tv_usec)*1e‑6;
    } /* end if */

  return(dtime);

} /* end getTimeInSec */

The precision of gettimeofday() varies with hardware but is generally good. The conversion to double precision in seconds may even reduce the timer’s precision, but not enough to affect the tests performed here.

The main routine runs both findMax() and findMaxVec() in an iteration loop (Listing 6), with calls to getTimeInSec() to time all iterations. The average runtime is computed from this overall duration, smoothing out any fast or slow runs of the functions. Variability in the runtime of individual calls is difficult to avoid in any complex operating system. The number of iterations can be tuned to get multiple seconds of runtime, at minimum, to ensure a good average.

Listing 6: Timing Loops

time1 = getTimeInSec();
  for(n=0;n<TIME_ITER;n++)
    {
      mret = findMax(N,xval);
    } /* end for n */
  duration = getTimeInSec() ‑ time1;

  time1 = getTimeInSec();
  for(n=0;n<TIME_ITER;n++)
    {
      mret = findMaxVec(N,xval);
    } /* end for n */
  duration = getTimeInSec() ‑ time1;

Metrics

Although you could use the total measured times to report the average runtime per iteration, that information will only allow you to evaluate equivalent versions of the same algorithm. To get a more general sense of performance, you can also compute an estimate of the operations performed per second by the code. This estimate should only include the operations in the algorithm itself. The computer is performing additional logistical operations, such as moving memory and controlling iteration loops, but these can be considered overhead. To optimize the code, this overhead should be reduced as much as feasible to concentrate the computer’s efforts on the actual work of the algorithm.

The operations count for the algorithm does not have to be absolutely accurate, although it should be a reasonable estimate. However, a consistent estimate will be more useful than one that adapts to the peculiarities of a particular processor. In the algorithm here, the polynomial evaluation involves five multiplies and three additions for each input value. The max and argmax functions are implemented by a single conditional if statement per input in the processing loop. The code estimates the multiplications and additions as one operation each, and the conditional as four operations (compare, conditional jump, operation, bad branch prediction), which gives the basic equation for the operations count,

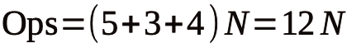
where N is the number of elements in the array. Dividing this by the runtime gives operations per second (Ops/s), which is scaled to giga-operations per second (GOps/s, or 1x109 Ops/s):

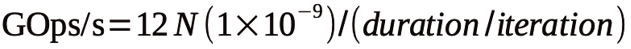
The use of the processor’s clock rate to compute the operations per clock (Ops/clk) gives a sense of the code’s processing efficiency:

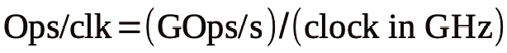
Because I did not include any overhead in the operations estimate, you would expect scalar code to execute not much more than one operation per clock and the NEON code no more than four operations per clock. As you will see, this rule of thumb is oversimplified but does provide an intuitive limit for initial assessment.

In addition to the computational rate, the memory access rate of the code should be estimated, as well. Comparing the code’s access rate to the computer’s memory bandwidth will help identify whether an implementation is memory limited or compute limited. For each iteration, the scalar and vector C code access the input array only once to compute the pair of output values (max, index). All other operations are carried out on data stored in registers or lower level cache memory, which means you can estimate the memory access from the array size in bytes divided by the time per iteration:

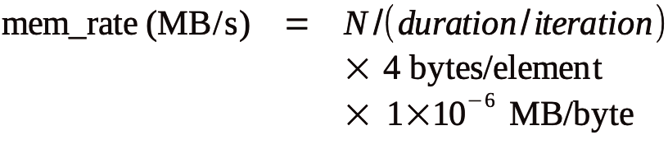
Compile the Code

The neontut.c code in Listing 9 can be compiled with gcc on ARM computers with NEON capability. Check your CPU’s documentation or look at the feature flags in the /proc/cpuinfo file to see if your ARM has NEON support (check for neon or asimd).

This tutorial is simple enough that you can call gcc directly. The -O3 flag selects relatively good, but safe, compiler optimizations. The -Wall flag enables extra compiler warnings. If you have a 32-bit ARM processor, you might need an additional flag to enable NEON instructions (-mfpu=neon). After compilation, you can run the code by calling neontut from the command line. The code will take some time to run the tests before displaying the scalar and vector results (Listing 7).

Listing 7: Compile and Run

$ gcc ‑O3 ‑Wall ‑o neontut neontut.c
$ ./neontut
Scalar: index = 2557, max = 119.098816, 
duration = 4.190763 msec
        rate = 3.002538 GOps/s, memory = 1000.845954 MB/s
Neon: index = 2557, max = 119.098824, 
duration = 2.392712 msec
        rate = 5.258854 GOps/s, memory = 1752.951308 MB/s

Python Comparison Code

For another point of reference, you can build the same algorithm in a high-level language. In Python, the findMax() function can be accomplished in just a few lines with two numpy functions (Listing 8). The test routine functionality also has been duplicated, with iterations timed by time.perf_counter(). Note that it expressly declares the input array as 32-bit floating point for the best comparison to the C code.

Listing 8: cmp2neon.py

01 import numpy as np
02 import time
03 
04 def findMax(xval):
05   P = [0.052, 0.24, 3.3, 10.1]
06   y = np.polyval(P,xval)
07   mxind = np.argmax(y)
08 
09   return (y[mxind],mxind)
10 
11 #end findMax
12 
13 if __name__ == "__main__":
14   TIME_ITER = 1000
15   N = 1024*1024+1
16 
17   # Generate matching random sequence
18   tmp = np.round(np.random.rand(N)*20e4)*5.0e‑5
19   xval = tmp.astype(np.float32)
20 
21   time1 = time.perf_counter()
22   for n in range(TIME_ITER):
23     (mxval,mxind) = findMax(xval)
24   #end for n
25   duration = time.perf_counter() ‑ time1
26   rate = TIME_ITER*N*12e‑9/duration
27   membw = TIME_ITER*N*12e‑6/duration
28 
29   print("Python: index = %d, max = %f, duration = %f msec" % (mxind,mxval,1.0e3*duration/TIME_ITER))
30   print("        rate = %f GOps/s, memory = %f MB/s" %(rate,membw))
31 
32 #end if main

One consequence of the Python implementation is additional memory access. The return from np.polyval() must write a second array, which is then read by np.argmax(). This results in at least three accesses of a memory array equal to the input size. The estimate for memory access in the Python implementation is:

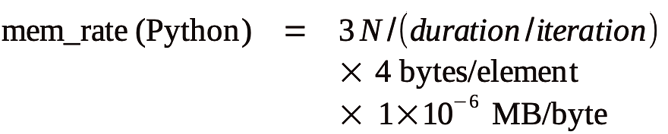
Results

Table 1 summarizes the statistics of the hardware used in the test, with the code run on three different ARM platforms (Raspberry Pi 4B and 5 and NVIDIA Jetson Nano). All tests were run on the systems with no other active user processes.

Some manufacturers will list the memory bandwidth for their processors, but you can also estimate this value by timing memory access operations. I do not address this topic in detail here because the reported memory rates are well below the memory bandwidth of each system, which indicates that all tests are compute-bound rather than memory-bound, and I can instead focus on the computational trends.

Tables 2, 3, and 4 summarize the test results for all three computers on the basis of time per iteration. Looking at the scalar C code first, you can see it has unusually high operations per clock ratios, even exceeding the notional one operation per clock limit on the RPi4 and RPi5. So high were these estimates that it warranted double-checking that the code was processing the entire array. Remember, however, that the computational model was not entirely accurate, so you are likely seeing some consequences of that. Unlike some processors, the ARM can use multiply-accumulate instructions even in scalar code, so it is getting a boost compared with the model. The conditional in the max operator is also overcounted by the model. The vast majority of the conditional operations will be comparing small values with a larger one because it isolates the maximum, meaning operations inside the if statement are not executed very often.

These discrepancies in the model would not normally be so obvious except that this code has very little overhead. The processor needs to shuffle around few variables for the algorithm to work, and most of the operations are the core math. Code, in general, exhibits much more overhead. As such, you should not use the results from this algorithm as a general benchmark, but rather to measure the improvement from the NEON instructions.

The results clearly show that the extra work involved in coding for NEON was not in vain. Even on the Raspberry Pi computers, where the scalar code optimized extremely well, NEON acceleration is 1.8 to 2.3 times, which is far from the ideal four times speedup one could expect, but as you saw, the NEON code has more overhead than the scalar code. The NEON code has a mix of scalar and vector variables, with conversions in between. It must also keep track of the vector and scalar indices separately. Lastly, it contained the additional cleanup section to match the scalar functionality exactly.

These additional costs reduce the gains made by the vector processing, but you still end up with substantial improvements, with roughly two times the performance from the NEON code on the same hardware. Although it costs extra time and attention in the development of the code, it is a one-time expense that pays dividends in significantly reduced runtimes for the lifetime of the code.

Your hardware also gets a new lease on life. As you can see from the tables, the RPi4 NEON code is only 16 percent slower than the scalar code on the RPi5, which would allow the NEON code to compete on hardware a full generation older than modern alternatives that use scalar code.

The tests for the Jetson Nano provide some additional insight. The scalar C code is two to three times less efficient than on the RPi4 or 5, which could be a result of a different compiler and optimizer version, or it could be indicative of improvements in the instruction per clock (IPC) of the newer ARM architectures (the Nano is an older processor).

The NEON code on the Jetson provides more than three times acceleration over the scalar code. Unlike the scalar code, the operations per clock figure of the NEON code on the Jetson is comparable to that of the RPi4. When coded with NEON intrinsics, the compiler gets more explicit directions on which instructions to use, reducing the amount of freedom the optimizer has to function. Although you do introduce an element of risk, you see it clearly benefits the code when done correctly.

In contrast with the Nano and RPi4, the operations per clock dramatically improve with the NEON code on the RPi5, which might be an indication of improvements made to the NEON units in the RPi5’s processing cores.

In all cases, the Python code was many times slower than even the scalar code. Only on the Jetson, where the scalar C code was much less efficient, was the Python code even close, being 2.5 times slower. The low overhead achieved in the C code is less possible with a higher level language that uses more generic and complex data structures. If you assume the two numpy routines are compiled functions under the hood, they still have additional overhead traversing in and out of the Python environment. The Python code must also manage an intermediate array and cannot conveniently combine the separate polynomial and argmax loops.

Considering all these factors, you can start to see why the Python code falls behind the scalar C code in this instance. The NEON code looks truly impressive by comparison, but you must be careful not to draw too many conclusions from this part of the tests. This algorithm is too specialized. Comparisons of C and Python performance with the use of more complex algorithms will have dramatically different results, dependent on the algorithms.

Conclusion

In this article, I touched on the usage of ARM’s SIMD capabilities, demonstrated how to integrate NEON instructions into C code, and measured the potential improvements it can bring to computational performance. In all cases, the NEON code produced truly impressive processing rates on very low power ARM processors. Table 5 summarizes all of the NEON instructions used in the findMaxVec() function, but so much more capability is available.

A number of resources are available for NEON instructions. ARM’s list of NEON intrinsics is complete but can lack detail on the instructions’ operations. ARM’s NEON introduction to developers has some general descriptions but is not extensive. Additionally, you can mimic Intel SSE and AltiVec code examples by converting to NEOwN-equivalent instructions. These SIMD implementations (for x86 and PowerPC, respectively) have a lot in common with ARM’s implementation, so coding techniques are highly transferable (with exceptions).

Listing 9: neontut.c

001 /* neontut.c ‑ A tutorial demonstrating the use
002  * of NEON intrinsic functions from the C language.
003  */
004 
005 #include <stdio.h>
006 #include <stdlib.h>
007 #include <stdint.h>
008 #include <memory.h>
009 #include <time.h>
010 #include <sys/time.h>
011 
012 #include <arm_neon.h>
013 
014 /* Define timing iteration count */
015 #define TIME_ITER 5000
016 
017 typedef struct{
018                 int   ind;
019                 float val;
020               } maxret_t;
021 
022 /* Function to return clock time in seconds */
023 static inline double getTimeInSec(void)
024 {
025   double dtime = ‑1.0;
026   struct timeval tv;
027 
028   if(gettimeofday(&tv,NULL) == 0)
029     {
030       dtime = ((double) tv.tv_sec) + ((double) tv.tv_usec)*1e‑6;
031     } /* end if */
032 
033   return(dtime);
034 
035 } /* end getTimeInSec */
036 
037 /* Prototypes to the test functions,
038  * code located after main routine
039  */
040 maxret_t findMax(int N, float *xval);
041 maxret_t findMaxVec(int N, float *xval);
042 
043 int main(int argc, char *argv[])
044 {
045   int n;
046   int N = 1024*1024 + 1;
047   size_t msize;
048   maxret_t mret = {‑1,0.0};
049   float *xval = NULL;
050   double time1, duration;
051   double rate, membw;
052 
053   /* Nlimit*sizeof(float) = 1GB */
054   const int Nlimit = 256*1024*1024;
055 
056   /* Parse command line argruments for
057    * simple experimentation
058    */
059   for(n=1;n= argc)
069             {
070               printf("‑n option requires integer argument\n");
071               return(‑1);
072             } /* end if */
073           else
074             {
075               N = atoi(argv[n]);
076             } /* end else n argument */
077         } /* end else if ‑n */
078       else
079         {
080           printf("Unknown argument [%s] ignoring\n",argv[n]);
081         } /* end else */
082     } /* end for n */
083 
084   /* Check value of N */
085   if(N < 0) N = 0;
086   if(N > Nlimit) N = Nlimit;
087 
088   /* Allocate the X value array.
089    * Unlike some SIMD, NEON appears to be
090    * compatible with 4‑byte alignment so we
091    * can use the standard malloc call.
092    *
093    * Rederiving N from msize is somewhat overcautious
094    * to protect against unexpected size_t conversion.
095    */
096   msize = ((size_t) N)*sizeof(float);
097   N = (int) msize/sizeof(float);
098   xval = (float *) malloc(msize);
099   if(xval == NULL)
100     {
101       fprintf(stderr,"Memory allocation error: %s:%d\n",__FILE__,__LINE__);
102       return(‑1);
103     } /* end if */
104 
105   /* Load xval with random floating‑point
106    * data between 0.00005 and 10
107    */
108   srand((unsigned int) time((time_t *) NULL));
109   for(n=0;n<N;n++)
110     {
111       xval[n] = ((float) (rand()%200000))*5.0e‑5;
112     } /* end for n */
113 
114   /* Run the scalar and vector functions
115    * multiple times to get good timings
116    */
117 
118   time1 = getTimeInSec();
119   for(n=0;n<TIME_ITER;n++)
120     {
121       mret = findMax(N,xval);
122     } /* end for n */
123   duration = getTimeInSec() ‑ time1;
124   rate = ((double) TIME_ITER)*((double) N)*12.0e‑9;
125   rate /= duration;
126   membw = ((double) TIME_ITER)*((double) N)*4.0e‑6;
127   membw /= duration;
128 
129   printf("Scalar: index = %d, max = %f, duration = %f msec\n", mret.ind,mret.val, 1e3*duration/((double) TIME_ITER));
130   printf("        rate = %f GOps/s, memory = %f MB/s\n", rate, membw);
131 
132   time1 = getTimeInSec();
133   for(n=0;n<TIME_ITER;n++)
134     {
135       mret = findMaxVec(N,xval);
136     } /* end for n */
137   duration = getTimeInSec() ‑ time1;
138   rate = ((double) TIME_ITER)*((double) N)*12.0e‑9;
139   rate /= duration;
140   membw = ((double) TIME_ITER)*((double) N)*4.0e‑6;
141   membw /= duration;
142 
143   printf("Neon: index = %d, max = %f, duration = %f msec\n", mret.ind,mret.val, 1e3*duration/((double) TIME_ITER));
144   printf("        rate = %f GOps/s, memory = %f MB/s\n", rate, membw);
145 
146   if(xval != NULL) free((void *) xval);
147   return(0);
148 
149 } /* end main */
150 
151 /* Scalar version of the test function */
152 maxret_t findMax(int N, float *xval)
153 {
154   int n;
155   float x, x2, x3;
156   float val;
157   maxret_t mret = {‑1, ‑1.0e38};
158 
159   const float A = 0.052;
160   const float B = 0.24;
161   const float C = 3.3;
162   const float D = 10.1;
163 
164   for(n=0;n<N;n++)
165     {
166       x = xval[n];
167       x2 = x*x;
168       x3 = x2*x;
169       val = A*x3 + B*x2 + C*x + D;
170 
171       if(val > mret.val)
172         {
173           mret.val = val;
174           mret.ind = n;
175         } /* end if */
176     } /* end for n */
177 
178   return(mret);
179 
180 } /* end findMax */
181 
182 /* Neon version of the test function */
183 maxret_t findMaxVec(int N, float *xval)
184 {
185   int n;
186   int Nv = N/4;
187 
188   float32x4_t vx, vx2, vx3;
189   float32x4_t vtmp;
190   float32x4_t *vxa = (float32x4_t *) xval;
191   float       vfload[4] __attribute__((aligned(16)));
192   int32_t     viload[4] __attribute__((aligned(16)));
193 
194   uint32x4_t  vmask;
195   float32x4_t vmax;
196   int32x4_t   vmxind;
197   int32x4_t   vind = {0, 1, 2, 3};
198   int32x4_t   vinc = {4, 4, 4, 4};
199 
200   maxret_t mret = {‑1, ‑1.0e‑38};
201 
202   const float32x4_t vA = {0.052, 0.052, 0.052, 0.052};
203   const float32x4_t vB = {0.24, 0.24, 0.24, 0.24};
204   const float32x4_t vC = {3.3, 3.3, 3.3, 3.3};
205   const float32x4_t vD = {10.1, 10.1, 10.1, 10.1};
206 
207   vmax = vdupq_n_f32(mret.val);
208   vmxind = vdupq_n_s32(mret.ind);
209   for(n=0;n mret.val) ||
255           ((vfload[n] == mret.val) &&
256            (viload[n] < mret.ind)) )
257         {
258           mret.val = vfload[n];
259           mret.ind = viload[n];
260         } /* end if */
261     } /* end for n */
262 
263   return(mret);
264 
265 } /* end findMaxVec */